MRCpy.DWGCS

class MRCpy.DWGCS(loss='0-1', deterministic=True, random_state=None, fit_intercept=False, D=4, sigma_=None, B=1000, solver='adam', alpha=0.01, stepsize='decay', mini_batch_size=None, max_iters=None, weights_beta=None, weights_alpha=None, phi='linear', **phi_kwargs)

Double-Weighting for General Covariate Shift

This class implements the Double-Weighting for General Covariate Shift (DW-GCS) method proposed in [1]. It is designed for supervised classification under covariate shift, where the marginal distributions of instances at training \(\mathrm{p}_{\text{tr}}(x)\) and testing \(\mathrm{p}_{\text{te}}(x)\) differ but the label conditionals coincide.

The classifier solves the minimax risk problem:

\[\mathrm{h}^{\mathcal{U}_2} \in \arg\min_{\mathrm{h}} \max_{\mathrm{p} \in \mathcal{U}_2} \ell(\mathrm{h}, \mathrm{p})\]

which finds the classifier \(\mathrm{h}\) that minimizes the worst-case expected loss over an uncertainty set \(\mathcal{U}_2\) of distributions.

The uncertainty set \(\mathcal{U}_2\) is constructed using both training weights \(\beta(x)\) and testing weights \(\alpha(x)\), with feature mappings weighted by \(\alpha(x)\) as \(\Phi_\alpha(x,y) = \alpha(x) \Phi(x,y)\):

\[\mathcal{U}_2 = \left\{ \mathrm{p} : \mathrm{p}_x = \mathrm{p}_{\text{te}}(x), \; \left| \mathbb{E}_{\mathrm{p}}[\Phi_\alpha(x,y)] - \boldsymbol{\tau} \right| \leq \boldsymbol{\lambda} \right\}\]

where \(\boldsymbol{\tau}\) is estimated using \(\beta\)-weighted training samples as \(\boldsymbol{\tau} = \frac{1}{n} \sum_{i=1}^{n} \beta(x_i) \Phi(x_i, y_i)\), and \(\boldsymbol{\lambda}\) is obtained by solving a convex optimization that ensures the uncertainty set is non-empty.

The double-weighting approach avoids the limitations of the reweighted methods (which only weight training samples by \(\mathrm{p}_{\text{te}}/\mathrm{p}_{\text{tr}}\)) and robust methods (which only weight testing samples by \(\mathrm{p}_{\text{tr}}/\mathrm{p}_{\text{te}}\)). By using both weights, DW-GCS can handle general covariate shift scenarios where the supports of training and testing distributions do not need to contain each other.

The weights \(\alpha(x)\) and \(\beta(x)\) are obtained by solving a Double-Weighting Kernel Mean Matching (DW-KMM) problem. The hyperparameter D controls the trade-off between estimation error and prediction confidence: the estimation error is of order \(\mathcal{O}(1/\sqrt{Dn})\), so larger D increases the effective sample size by a factor of D compared with reweighted methods.

It implements 0-1 and log loss, and can be used with linear, Random Fourier, and ReLU features.

See [1] for further details.

Parameters:

lossstr {‘0-1’, ‘log’}, default = ‘0-1’

Type of loss function to use for the risk minimization. 0-1 loss quantifies the probability of classification error at a certain example for a certain rule. Log-loss quantifies the minus log-likelihood at a certain example for a certain rule.

deterministicbool, default = True

Whether the prediction of the labels should be done in a deterministic way (given a fixed random_state in the case of using random Fourier or random ReLU features).

random_stateint, RandomState instance, default = None

Random seed used when ‘fourier’ and ‘relu’ options for feature mappings are used to produce the random weights.

fit_interceptbool, default = False

Whether to calculate the intercept for MRCs. If set to false, no intercept will be used in calculations (i.e. data is expected to be already centered).

Dint, default = 4

Hyperparameter that controls the trade-off between error in expectation estimates and confidence of the classification. The weights are computed using \(C = B / \sqrt{D}\). Larger values of D reduce estimation error (effective sample size increases by factor D) but may reduce prediction confidence for testing instances unlikely at training.

• D=1: Only training weights \(\beta(x)\) are used (reweighted approach, \(\alpha(x) = 1\)).

• D=inf: Only testing weights \(\alpha(x)\) are used (robust approach, \(\beta(x) = 1\)).

• 1 < D < inf: Both weights are used (double-weighting).

Bint, default = 1000

Upper bound on the maximum value of the training weights \(\beta(x)\). Used in the DW-KMM optimization to constrain \(\beta(x) \leq B / \sqrt{D}\).

solver{‘cvx’, ‘grad’, ‘adam’}, default = ‘adam’

Method to use in solving the optimization problem. Default is ‘adam’. To choose a solver, you might want to consider the following aspects:

‘cvx’

Solves the optimization problem using the cvxpy library. Obtains an accurate solution while requiring more time than the other methods. Note that the library uses the GUROBI solver in cvxpy for which one might need to request for a license. A free license can be requested here

‘grad’

Solves the optimization using stochastic gradient descent. The parameters max_iters, stepsize and mini_batch_size determine the number of iterations, the learning rate and the batch size for gradient computation respectively. Note that the implementation uses nesterov’s gradient descent in case of ReLU and threshold features, and the above parameters do not affect the optimization in this case.

‘adam’

Solves the optimization using stochastic gradient descent with adam (adam optimizer). The parameters max_iters, alpha and mini_batch_size determine the number of iterations, the learning rate and the batch size for gradient computation respectively. Note that the implementation uses nesterov’s gradient descent in case of ReLU and threshold features, and the above parameters do not affect the optimization in this case.

alphafloat, default = 0.001

Learning rate for ‘adam’ solver.

mini_batch_sizeint, default = 1 or 32

The size of the batch to be used for computing the gradient in case of stochastic gradient descent and adam optimizer. In case of stochastic gradient descent, the default is 1, and in case of adam optimizer, the default is 32.

max_itersint, default = 100000 or 5000 or 2000

The maximum number of iterations to use in case of ‘grad’ or ‘adam’ solver. The default value is 100000 for ‘grad’ solver and 5000 for ‘adam’ solver and 2000 for nesterov’s gradient descent.

weights_alphaarray, default = None

Pre-computed testing weights \(\alpha(x)\) associated to each testing instance. If only weights_alpha is given, the method fixes \(\beta(x) = 1\) (robust approach).

weights_betaarray, default = None

Pre-computed training weights \(\beta(x)\) associated to each training sample. If only weights_beta is given, the method fixes \(\alpha(x) = 1\) (reweighted approach).

phistr or BasePhi instance, default = ‘linear’

Type of feature mapping function to use for mapping the input data. The currently available feature mapping methods are ‘fourier’, ‘relu’, and ‘linear’. The users can also implement their own feature mapping object (should be a BasePhi instance) and pass it to this argument. Note that when using ‘fourier’ feature mapping, training and testing instances are expected to be normalized. To implement a feature mapping, please go through the Feature Mappings section.

‘linear’

It uses the identity feature map referred to as Linear feature map. See class BasePhi.

‘fourier’

It uses Random Fourier Feature map. See class RandomFourierPhi.

‘relu’

It uses Rectified Linear Unit (ReLU) features. See class RandomReLUPhi.

**phi_kwargsAdditional parameters for feature mappings.

Groups the multiple optional parameters for the corresponding feature mappings(phi).

For example in case of fourier features, the number of features is given by n_components parameter which can be passed as argument DWGCS(loss='log', phi='fourier', n_components=300)

The list of arguments for each feature mappings class can be found in the corresponding documentation.

See also

MRCpy.CMRC

CMRC using uncertainty set \(\mathcal{U}_2\) with marginal constraints [2].

References

[1] (1,2)

Segovia-Martín, J.I., Mazuelas, S., & Liu, A. (2023). Double-Weighting for Covariate Shift Adaptation. In Proceedings of the 40th International Conference on Machine Learning, pp. 30439-30457.

[2]

Mazuelas, S., Shen, Y., & Pérez, A. (2022). Generalized Maximum Entropy for Supervised Classification. IEEE Transactions on Information Theory, 68(4), 2530-2550.

Attributes:

is_fitted_bool

Whether the classifier is fitted i.e., the parameters are learnt.

beta_array-like of shape (n_train_samples, 1)

Training weights \(\beta(x)\) obtained from the DW-KMM optimization.

alpha_array-like of shape (n_test_samples, 1)

Testing weights \(\alpha(x)\) obtained from the DW-KMM optimization.

classes_array-like of shape (n_classes,)

Labels in the given dataset.

mu_array-like of shape (n_features,) or float

Parameters learnt by the optimization.

sigma_float

Kernel bandwidth parameter for the RBF kernel used in DW-KMM.

Methods

DWKMM(xTr, xTe)	Obtain training and testing weights.
error(X, Y)	Return the mean error obtained for the given test data and labels.
fit(xTr, yTr[, xTe])	Fit the MRC model.
get_metadata_routing()	Get metadata routing of this object.
get_params([deep])	Get parameters for this estimator.
get_upper_bound()	Returns the upper bound on the expected loss for the fitted classifier.
minimax_risk(X, tau_mat, lambda_mat, n_classes)	Solves the marginally constrained minimax risk optimization problem for different types of loss (0-1 and log loss).
predict(X)	Predicts classes for new instances using a fitted model.
predict_proba(X)	Computes conditional probabilities corresponding to each class for the given unlabeled instances.
psi(phi_mu, phi)	Function to compute the psi function in the objective using the given solution mu and the feature mapping corresponding to a single instance.
score(X, y[, sample_weight])	Return the mean accuracy on the given test data and labels.
set_fit_request(*[, xTe, xTr, yTr])	Request metadata passed to the fit method.
set_params(**params)	Set the parameters of this estimator.
set_score_request(*[, sample_weight])	Request metadata passed to the score method.

DWKMM(xTr, xTe)

Obtain training and testing weights.

Computes the weights associated to the training and testing samples solving the DW-KMM problem.

Parameters:

xTrarray-like of shape (n_samples, n_dimensions)

Training instances used for computing the training weights beta and testing weights alpha.

xTearray-like of shape (n_samples, n_dimensions)

Testing instances used for computing the training weights beta and testing weights alpha.

Returns:

self :

Fitted estimator with beta_ and alpha_ attributes set.

__init__(loss='0-1', deterministic=True, random_state=None, fit_intercept=False, D=4, sigma_=None, B=1000, solver='adam', alpha=0.01, stepsize='decay', mini_batch_size=None, max_iters=None, weights_beta=None, weights_alpha=None, phi='linear', **phi_kwargs)

Initialize self. See help(type(self)) for accurate signature.

error(X, Y)

Return the mean error obtained for the given test data and labels.

Parameters:

Xarray-like of shape (n_samples, n_dimensions)

Test instances for which the labels are to be predicted by the MRC model.

Yarray-like of shape (n_samples, 1), default=None

Labels corresponding to the testing instances used to compute the error in the prediction.

Returns:

errorfloat

Mean error of the learned MRC classifier

fit(xTr, yTr, xTe=None)

Fit the MRC model.

Computes the parameters required for the minimax risk optimization and then calls the minimax_risk function to solve the optimization.

Parameters:

xTrarray-like of shape (n_samples, n_dimensions)

Training instances used in

• Calculating the expectation estimates that constrain the uncertainty set for the minimax risk classification

• Solving the minimax risk optimization problem.

n_samples is the number of training samples and n_dimensions is the number of features.

yTrarray-like of shape (n_samples, 1), default = None

Labels corresponding to the training instances used only to compute the expectation estimates.

xTearray-like of shape (n_samples2, n_dimensions), default = None

These instances will be used in the minimax risk optimization. These extra instances are generally a smaller set and give an advantage in training time.

Returns:

self :

Fitted estimator

get_metadata_routing()

Get metadata routing of this object.

Please check User Guide on how the routing mechanism works.

Returns:

routingMetadataRequest

A MetadataRequest encapsulating routing information.

get_params(deep=True)

Get parameters for this estimator.

Parameters:

deepbool, default=True

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

paramsdict

Parameter names mapped to their values.

get_upper_bound()

Returns the upper bound on the expected loss for the fitted classifier.

Returns:

upper_boundfloat

Upper bound of the expected loss for the fitted classifier.

minimax_risk(X, tau_mat, lambda_mat, n_classes)

Solves the marginally constrained minimax risk optimization problem for different types of loss (0-1 and log loss). When use_cvx=False, it uses SGD optimization for linear and random fourier feature mappings and nesterov subgradient approach for the rest.

Parameters:

Xarray-like of shape (n_samples, n_dimensions)

Training instances used for solving the minimax risk optimization problem.

tau_array-like of shape (n_features * n_classes)

The mean estimates for the expectations of feature mappings.

lambda_array-like of shape (n_features * n_classes)

The variance in the mean estimates for the expectations of the feature mappings.

n_classesint

Number of labels in the dataset.

Returns:

self :

Fitted estimator

predict(X)

Predicts classes for new instances using a fitted model.

Returns the predicted classes for the given instances in X using the probabilities given by the function predict_proba.

Parameters:

Xarray-like of shape (n_samples, n_dimensions)

Test instances for which the labels are to be predicted by the MRC model.

Returns:

y_predarray-like of shape (n_samples,)

Predicted labels corresponding to the given instances.

predict_proba(X)

Computes conditional probabilities corresponding to each class for the given unlabeled instances.

Parameters:

Xarray-like of shape (n_samples, n_dimensions)

Testing instances for which the prediction probabilities are calculated for each class.

Returns:

hy_xarray-like of shape (n_samples, n_classes)

The conditional probabilities (p(y|x)) corresponding to each class.

psi(phi_mu, phi)

Function to compute the psi function in the objective using the given solution mu and the feature mapping corresponding to a single instance.

Parameters:

phi_muarray-like of shape (n_features,)

Product of feature mapping and solution vector.

phiarray-like of shape (n_classes, n_features)

Feature mapping corresponding to an instance and each class.

Returns:

garray-like of shape (n_features,)

Gradient of psi for a given solution and feature mapping.

psi_valuefloat

The value of psi for a given solution and feature mapping.

score(X, y, sample_weight=None)

Return the mean accuracy on the given test data and labels.

In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.

Parameters:

Xarray-like of shape (n_samples, n_features)

Test samples.

yarray-like of shape (n_samples,) or (n_samples, n_outputs)

True labels for X.

sample_weightarray-like of shape (n_samples,), default=None

Sample weights.

Returns:

scorefloat

Mean accuracy of self.predict(X) w.r.t. y.

set_fit_request(*, xTe: Union[bool, None, str] = '$UNCHANGED$', xTr: Union[bool, None, str] = '$UNCHANGED$', yTr: Union[bool, None, str] = '$UNCHANGED$') → MRCpy.dwgcs.DWGCS

Request metadata passed to the fit method.

Note that this method is only relevant if enable_metadata_routing=True (see sklearn.set_config()). Please see User Guide on how the routing mechanism works.

The options for each parameter are:

• True: metadata is requested, and passed to fit if provided. The request is ignored if metadata is not provided.

• False: metadata is not requested and the meta-estimator will not pass it to fit.

• None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.

• str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

New in version 1.3.

Note

This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a Pipeline. Otherwise it has no effect.

Parameters:

xTestr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED

Metadata routing for xTe parameter in fit.

xTrstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED

Metadata routing for xTr parameter in fit.

yTrstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED

Metadata routing for yTr parameter in fit.

Returns:

selfobject

The updated object.

set_params(**params)

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as Pipeline). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.

Parameters:

**paramsdict

Estimator parameters.

Returns:

selfestimator instance

Estimator instance.

set_score_request(*, sample_weight: Union[bool, None, str] = '$UNCHANGED$') → MRCpy.dwgcs.DWGCS

Request metadata passed to the score method.

Note that this method is only relevant if enable_metadata_routing=True (see sklearn.set_config()). Please see User Guide on how the routing mechanism works.

The options for each parameter are:

• True: metadata is requested, and passed to score if provided. The request is ignored if metadata is not provided.

• False: metadata is not requested and the meta-estimator will not pass it to score.

• None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.

• str: metadata should be passed to the meta-estimator with this given alias instead of the original name.

The default (sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.

New in version 1.3.

Note

This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a Pipeline. Otherwise it has no effect.

Parameters:

sample_weightstr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED

Metadata routing for sample_weight parameter in score.

Returns:

selfobject

The updated object.

Examples using MRCpy.DWGCS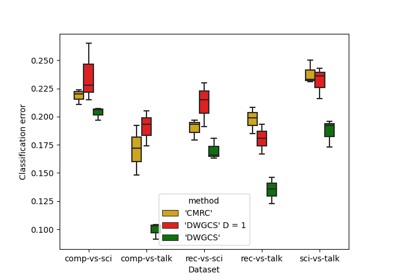

Example: Use of DWGCS (Double-Weighting General Covariate Shift) for Covariate Shift Adaptation

Example: Use of DWGCS (Double-Weighting General Covariate Shift) for Covariate Shift Adaptation